La passerelle du MIL : un réseau de diffraction acoustique
par Mathieu Villeneuve, Paul-Édouard Blanchard
Journal étudiant de la PHYSUM
par Mathieu Villeneuve, Paul-Édouard Blanchard
 FIGURE 1 - La section de la passerelle du MIL agissant comme un réseau de diffraction acoustique.
FIGURE 1 - La section de la passerelle du MIL agissant comme un réseau de diffraction acoustique.
Introduction
Certains utilisateurs de la station Acadie ont peut-être déjà remarqué qu'en traversant la section clôturée de la passerelle Marcelle-et-Jean-Coutu à pied, leurs pas sont étrangement suivis de brefs gazouillis.
En fait, les architectes chargés de son design ne réalisaient probablement pas qu'ils étaient en train de concevoir un réseau de diffraction plus grand que nature, suffisamment grand pour accommoder les ondes sonores.
Il est facile de comprendre le phénomène lorsque l'on constate que les poutres du garde-fou sont espacées par un intervalle régulier d'une dizaine de centimètres, qui s'avère être du même ordre de grandeur que la longueur d'onde d'un son de quelques milliers de Hertz. Cette géométrie leur confère la capacité d'agir individuellement comme des éléments réfléchissants et, collectivement, comme un réseau de diffraction acoustique.
Comment entendre l'effet?
La méthode optimale pour entendre l'effet de diffraction est de se placer au centre de la section d'intérêt de la passerelle - afin d'utiliser les deux fronts d'ondes voyageant vers le MIL et vers la station Acadie - et de générer un pulse au niveau du sol, en tapant du pied ou en demandant à un acolyte accroupi de taper des mains. Il est important que la source se trouve au ras du sol afin de pouvoir profiter du meilleur angle de réflexion vers les oreilles, situées plus en hauteur.
Qu'est-ce qu'un réseau de diffraction?
Selon le principe de Huygens-Fresnel, lorsqu'une onde rencontre un objet solide, chaque point de l'interface entre l'objet et le milieu de propagation agit comme la source d'une petite onde sphérique, que l'on appelle une ondelette. Au moment de se recombiner en un front d'onde unique, ces ondelettes, qui ont leur point d'origine en des positions différentes, interfèrent l'une avec l'autre de manière à former un patron de diffraction, c'est-à-dire un ensemble de directions de propagation où l'intensité de la lumière est plus faible (interférence destructive) ou plus élevée (interférence constructive).
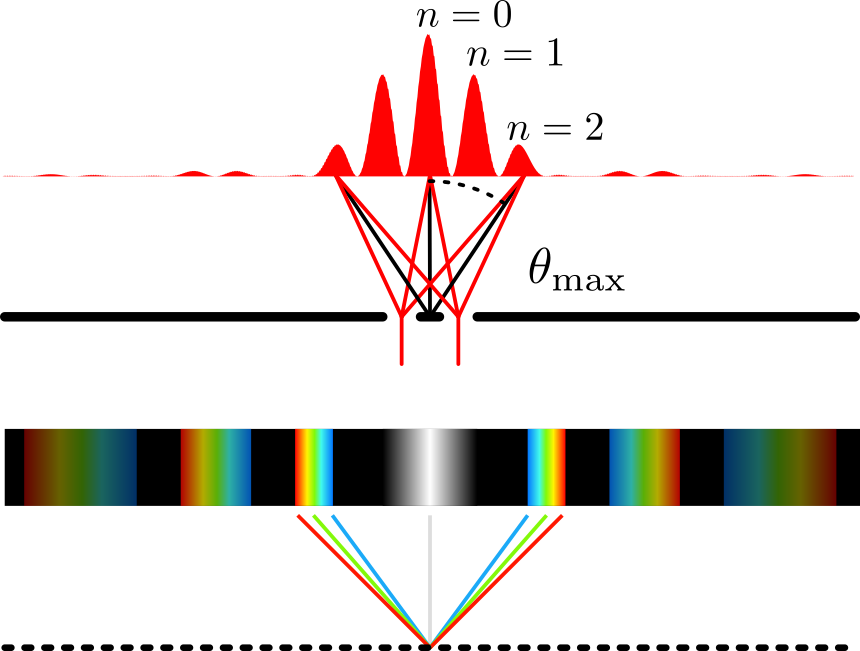
FIGURE 2 - Exemples de patrons de diffraction.
Haut : profil d'intensité lumineuse pour une lumière monochromatique et une double fente. θmax correspond à l'angle d'interférence parfaitement constructive, marquée par une intensité lumineuse maximale (note : ici, seul le θmax de l'ordre de diffraction n=2 est représenté).
Bas : réseau de diffraction et lumière polychromatique. Puisque chaque longueur d'onde possède un θmax différent, les franges lumineuses prennent l'aspect d'un arc-en-ciel.
L'un des cas les plus canoniques du phénomène est l'expérience de la double fente: deux fentes très minces diffractent une onde lumineuse incidente de manière à faire apparaître un patron de diffraction sur un écran réfléchissant situé un peu plus loin. En augmentant significativement le nombre de fentes et en réduisant leur espacement, on obtient un réseau de diffraction, l'un des dispositifs les plus importants en spectroscopie en raison de sa capacité à séparer efficacement le spectre de la lumière incidente.
Notons aussi que les fentes peuvent être remplacées par des éléments réfléchissants ; on parle alors de réseau de diffraction en réflexion plutôt qu'en transmission.
En progressant le long de la passerelle, le front d'onde est successivement réfléchi par les poutres de métal. Or, le délai entre l'instant d'incidence de l'onde sur une poutre et les suivantes introduit une certaine différence de phase relative entre chaque réflexion. En se recombinant sur le chemin du retour vers l'observateur, les réflexions ainsi déphasées les unes par rapport aux autres interfèrent ensemble de manière à créer un patron de diffraction dont l'origine se situe au point d'impact entre l'onde incidente et le garde-fou. Puisque la position du point d'impact n'est pas fixe, l'observateur intercepte successivement différentes parties du patron de diffraction. Il en résulte un glissement des fréquences entendues vers le bas.
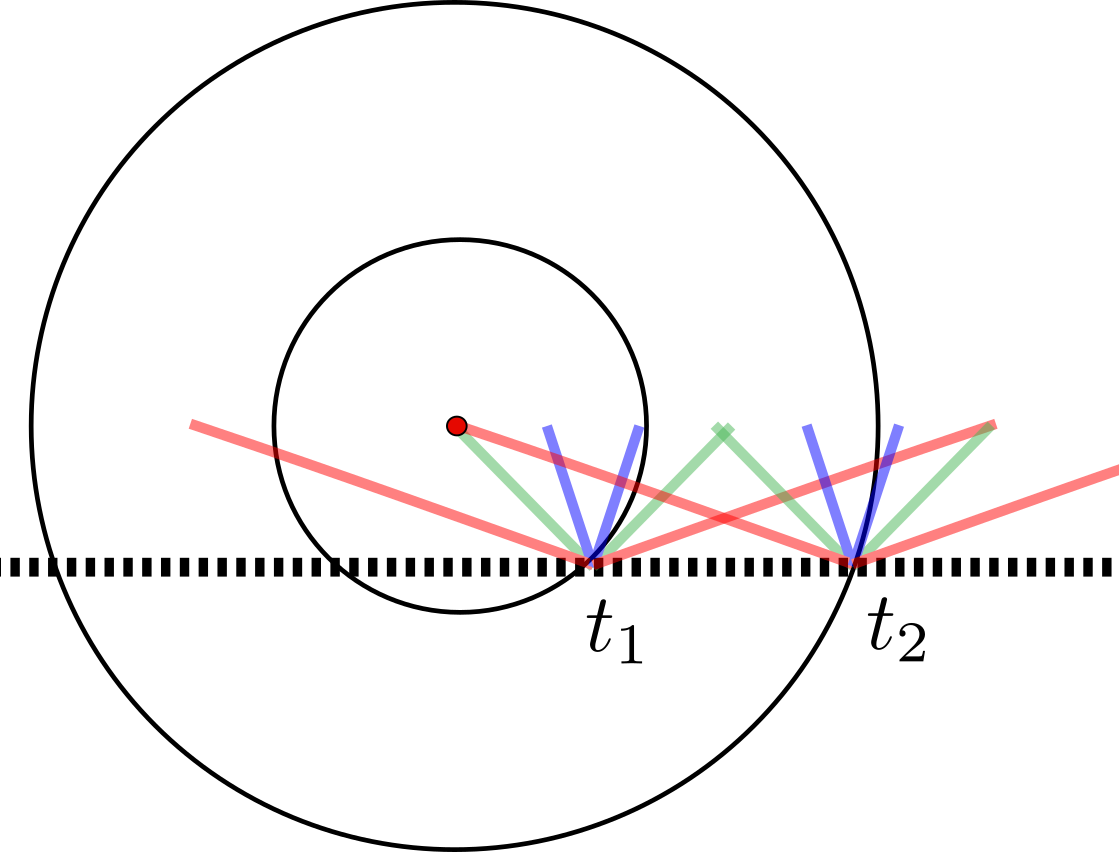
FIGURE 3 - Exemples de patrons de diffraction.
Schéma qualitatif de l'effet de diffraction. Le front d'onde (cercles noirs) voyage le long du réseau et forme un patron de diffraction à l'emplacement du point d'impact (motifs multicolores ; chaque couleur correspond à une fréquence). Puisque le point d'impact se déplace à la vitesse du son, l'observateur intercepte différentes fréquences aux instants t1 et t2. Il en résulte un glissement des fréquences entendues vers le bas. Note : la forme des patrons de diffraction n'est pas réaliste.
Le mécanisme est représenté schématiquement à la Figure 3.
Nous entreprenons maintenant de trouver une relation exprimant l'évolution temporelle des fréquences entendues suite à l'émission d'un son de claquement. Deux méthodes différentes sont utilisées : une première, basée sur la condition d'interférence constructive appliquée à un réseau unidimensionnel (communément appelée « loi de Bragg »), et une seconde, plus rigoureuse, reposant sur la transformée de Fourier de la convolution d'un pulse sonore et de la fonction de réponse de la passerelle.
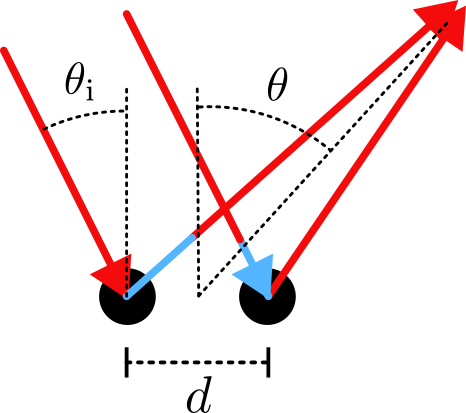
FIGURE 4 - Représentation schématique du déphasage menant à de l'interférence entre deux ondes (de longueur d'onde λ) réfléchies par des particules espacées d'une distance d. Les angles d'incidence et de sortie sont respectivement θi et θ. Les sections bleues sont les différences de longueur de parcours donnant lieu au déphasage. L'interférence parfaitement constructive est associée à l'angle de sortie θmax et survient lorsque la différence de distance parcourue atteint n λ, où n est un entier. On peut montrer que la condition d'interférence constructive s'énonce n λ = d (sinθi + sinθmax).
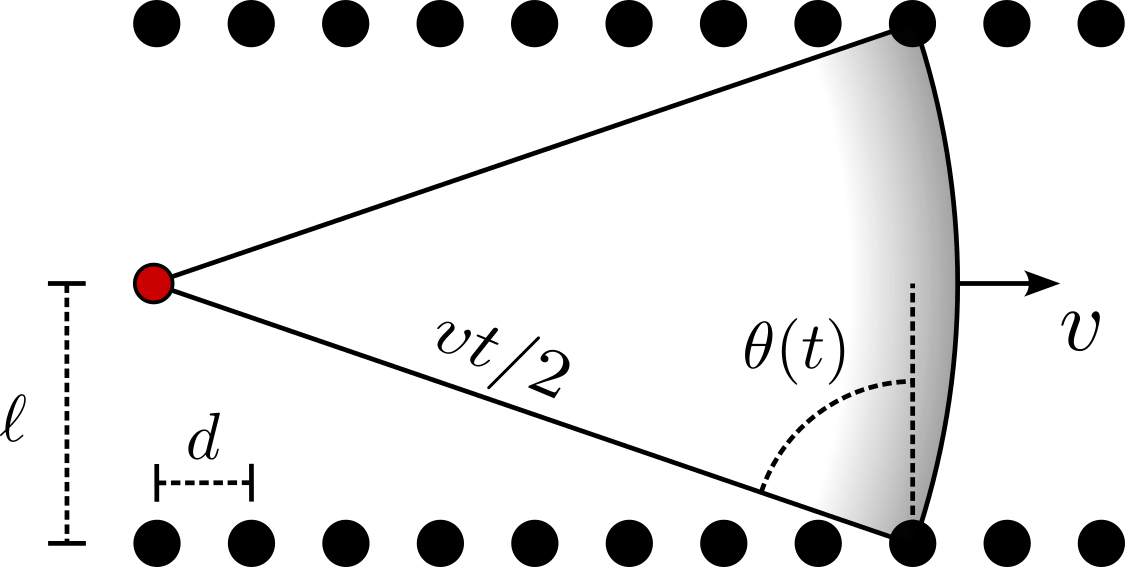
Figure 5 - Représentation de la géométrie du problème. Les poutres métalliques sont espacées d'une distance d et l'émetteur-récepteur se trouve à une distance perpendiculaire ℓ du garde-fou. L'angle d'incidence θ augmente à mesure que le pulse avance à la vitesse v. L'émetteur-récepteur est séparé du point de réflexion par une distance vt/2, où t est le temps d'aller-retour du pulse et est égal à son instant de réception.
Le modèle simple
On conçoit ici chaque poutre de métal comme l'élément d'un réseau de diffraction en réflexion. On peut assez facilement montrer, à partir d'arguments géométriques (voir la Figure 4), que pour un espacement d entre chaque élément du réseau, le nième ordre de diffraction pour une longueur d'onde λ est lié aux angles d'incidence θi et d'interférence parfaitement constructive θmax par la relation1 (Communément appelée « loi de Bragg »).
(1) n λ = d (sinθi + sinθmax)
Dans le cas de la diffraction sur la passerelle, dont la géométrie est illustrée à la Figure 5, on considère l'onde incidente comme un pulse spatialement cylindrique (la géométrie étant ici réduite à deux dimensions) d'une durée infiniment courte. On suppose également que la source sonore et l'observateur se trouvent au même endroit, conduisant à l'égalité θi = θmax = θ. L'équation (1) devient :
(2) n λ = 2 d sin θ
Enfin, puisque le pulse se propage dans l'espace à la vitesse du son v, on peut relier θ avec le temps t d'aller-réflexion-retour par la relation :
(3) θ(t) = arccos (2ℓ/v t)
Avec λ = v/f ainsi que l'identité trigonométrique sin (arccos x) = √(1 - x2), la substitution de l'équation (eqn:theta(t)) dans l'équation (eqn:bragg_passerelle) donne finalement la fréquence entendue au nième ordre de diffraction en fonction du temps :
(4) fn(t) = n v2 t / 2d √(v2 t2 - 4ℓ2)
La Figure 6 porte en graphique les quatre premiers ordres de l'équation (4) pour les valeurs numériques du tableau.
Les failles du modèle simple
Bien que l'équation (4) reproduit fidèlement le glissement des fréquences vers le bas, le modèle simple présente trois failles majeures.
.png)
Figure 6 - Les quatre premiers ordres de l'équation (4) pour les valeurs numériques énoncées dans le texte. Le glissement en fréquence caractéristique s'opère dans les 50 premières millisecondes et n'implique que la première quinzaine de mètres parcourus par le front d'onde.
Les deux premières, assez évidentes, sont que l'amplitude sonore n'est jamais considérée et que la géométrie demeure bidimensionnelle. La troisième, un peu plus subtile, est qu'il donne une relation exacte entre la fréquence et le temps, qui forment pourtant un couple de variables conjuguées par une transformée de Fourier. Or, un signal très localisé dans le temps se traduit par une distribution très délocalisée dans les fréquences et vice-versa. Il est donc impossible d'associer une valeur précise de fréquence à une valeur précise de temps.
Autrement dit, l'équation (4) viole le principe d'incertitude temps-fréquence qui, dans le cadre du traitement de signal, s'énonce par la limite de Gabor :
(5) σf σt ≥ 1 / 4 π
où σf et σt sont les écarts-types respectifs des distributions fréquentielles et temporelles.
Le modèle simple se plaçait dès le départ dans la perspective du domaine fréquentiel ; le signal était implicitement conçu comme une distribution (constante) de fréquences. Nous élaborerons dans ce qui suit un modèle qui reste dans le domaine temporel et qui a comme objectif d'obtenir un signal réaliste d'amplitude en fonction du temps. Le concept de fréquence ne se sera introduit qu'à la toute fin, indirectement, au moment de calculer la transformée de Fourier du signal.
Les ondes acoustiques sont de petites variations longitudinales de la pression atmosphérique, que l'on notera p. Elles obéissent à l'équation d'onde c2 ∇2 p = ¨p qui, en coordonnées sphériques, admet comme solution générale p(r, t) = p0 ei(kr - ωt) / r + c.c., c'est-à-dire une onde sphérique.
Il en découle que toute onde progressive sphérique peut s'écrire comme le produit d'un certain profil φ(r - ct) et d'une amplitude décroissante en 1/r :
(6) p(r, t) = p0 φ(r - ct) / r

Figure 7 - Géométrie de la réflexion sur une poutre. Les paramètres sont les suivants (gauche à droite). ymin et ymax : hauteurs des deux extrémités de la poutre. y : position verticale du point de réémission d'une ondelette (agissant ici comme la variable). m : indice de l'élément du réseau (la mième poutre). ral et rre : distances d'aller et de retour du pulse réfléchis au point y. xm : distance horizontale entre la source et la poutre (voir la Figure 5). hobs et hsou : hauteurs de la source et de l'observateur.
Le point de départ du modèle convolutif est de considérer le pulse acoustique initial comme une telle onde sphérique. En se propageant le long de la passerelle, ce pulse est réfléchi par les poutres métalliques dans toutes les directions. Le principe de Huygens-Fresnel nous inspire ici à concevoir chaque point de réflexion comme la source ponctuelle d'une petite ondelette sphérique de même profil que l'onde originale. C'est en additionnant ces ondelettes réfléchies par chaque point du réseau que nous parviendrons à reconstruire le signal d'amplitude en fonction du temps. Pour ce faire, il faudra trouver à quel moment les réflexions successives du pulse initial parviennent à l'observateur et quel type de transformation s'applique à leurs amplitudes.
Notons ici que le modèle convolutif se base sur la théorie de la réponse linéaire, qui est un sujet assez avancé de la physique et dont l'idée générale est de décrire comment un système réagit à un signal d'entrée pour produire un signal de sortie. Il est donc normal que des concepts tels que la fonction de réponse et la convolution soient étrangers à certains lecteurs. Ces sujets sont toutefois étudiés en profondeur dans le cours de troisième année « Électromagnétisme avancé » (PHY 3442) dans le contexte de la réponse d'un milieu diélectrique à la radiation électromagnétique incidente.
La fonction de réponse de la passerelle
Soit ral et rre, les distances respectives d'aller et de retour parcourues par l'onde au cours d'un trajet reliant sa source, une particule solide réfléchissante et l'oreille de l'observateur. Comme l'indique l'équation (eqn:onde_sphérique), l'amplitude de l'onde est réduite d'un facteur 1/ral suite à son parcours jusqu'à un point de réflexion. L'ondelette réémise de ce point possède donc une amplitude initiale1p0/ral et finale p0 / (ral rre), le trajet du retour ayant ajouté un facteur 1/rre supplémentaire. La valeur de t associée à sa réception par l'observateur est quant à elle t = (ral + rre) / v.
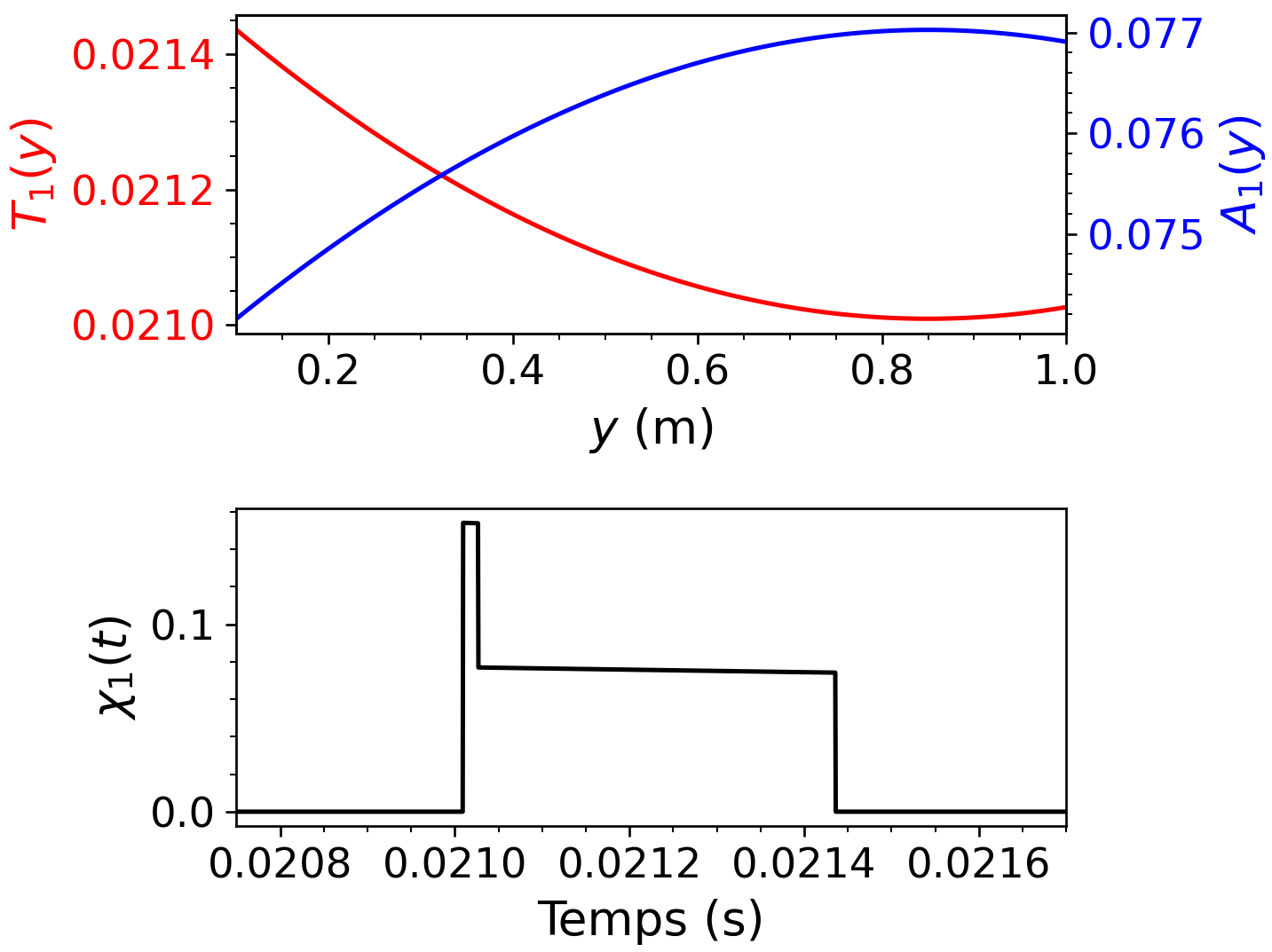
Figure 8 - Haut : courbes de Am(y) et Tm(y) pour m = 1. On voit bien que deux valeurs de y distinctes existent pour 0.0210 ≤ Tm ≤ 0.02105. Bas : fonction de réponse χm(t) pour m = 1. La protubérance au côté gauche démarque les valeurs de t pour lesquelles les ondelettes émises de deux positions y différentes parviennent à l'observateur en même temps.
Nous considérons donc chaque poutre métallique comme un continuum vertical de particules réflectives, dont la géométrie est représentée à la Figure fig:reflexion_poutre. Il devient alors possible de définir, pour chaque poutre d'indice m, le délai de réception Tm(y) de l'ondelette réfléchie du point y ainsi qu'une certaine fonction Am(y) exprimant son amplitude relative p/p0 perçue par l'observateur. Ces deux fonctions s'écrivent :
\[ A_m(y) = \left\{ \begin{array}{ll} \left( r_{\text{al},m} \, r_{\text{re},m}\right)^{-1} & \text{si} \ y_{\text{min}} \leq y \leq y_{\text{max}} \\ 0 & \text{autrement} \end{array} \right. \]
\[ T_m(y) = \frac{r_{\text{al},m}+r_{\text{re},m}}{v} \]
avec (voir les Figures (5) et (7)) :
ral,m = √(xm2 + (y - hsou)2)
rre,m = √(xm2 + (hobs - y)2)
xm = √(ℓ2 + m2 d2)
Cependant, nous nous intéressons ultimement à la construction d'un signal d'amplitude paramétré par le temps, pas à un couple de fonctions distinctes d'amplitude et de temps paramétrées par y. Nous devons donc inverser l'équation (8) pour trouver ym(t), puis l'insérer dans l'équation (7).
Cette opération nous conduit à obtenir χm(t), la fonction de réponse du mième élément du réseau. La Figure 8 montre les courbes de Tm(y), Am(y) et χm(t) pour m = 1.
En additionnant la contribution de chaque poutre, on trouve la fonction de réponse totale de la passerelle :
χ(t) = ∑m χm(t)
Calcul numérique de χm(t)
Tm(y) est une hyperbole tronquée. Par conséquent, son inverse n'est techniquement pas une fonction, car certaines valeurs de Tm correspondent à deux valeurs de y. L'inversion consiste donc à tout d'abord définir une maille régulière de valeurs discrètes de temps {ti} (espacées de Δt), puis à résoudre numériquement l'équation Tm(y) - ti = 0 pour chaque ti, en ne conservant que les solutions comprises entre ymin et ymax.
Si deux solutions existent pour un certain ti, la fonction de réponse doit tenir compte de ces deux contributions. Physiquement, cela signifie que les ondelettes réémises de deux positions y différentes atteignent l'observateur en même temps ; il faut donc additionner les deux amplitudes.
On peut définir la fonction de réponse à l'aide de l'algorithme suivant :
Deux solutions ym(1)(ti) et
ym(2)(ti) dans l'intervalle
ym(j)(ti) ∈ [ymin,
ymax]
χm(ti) = Am(ym(1)(ti)) + Am(ym(2)(ti))
Une seule solution ym(ti) dans l'intervalle ym(ti) ∈ [ymin, ymax]
χm(ti) = Am(ym(ti))
Aucune solution dans l'intervalle ym(ti) ∈ [ymin, ymax]
χm(ti) = 0
Convolution et spectrogramme
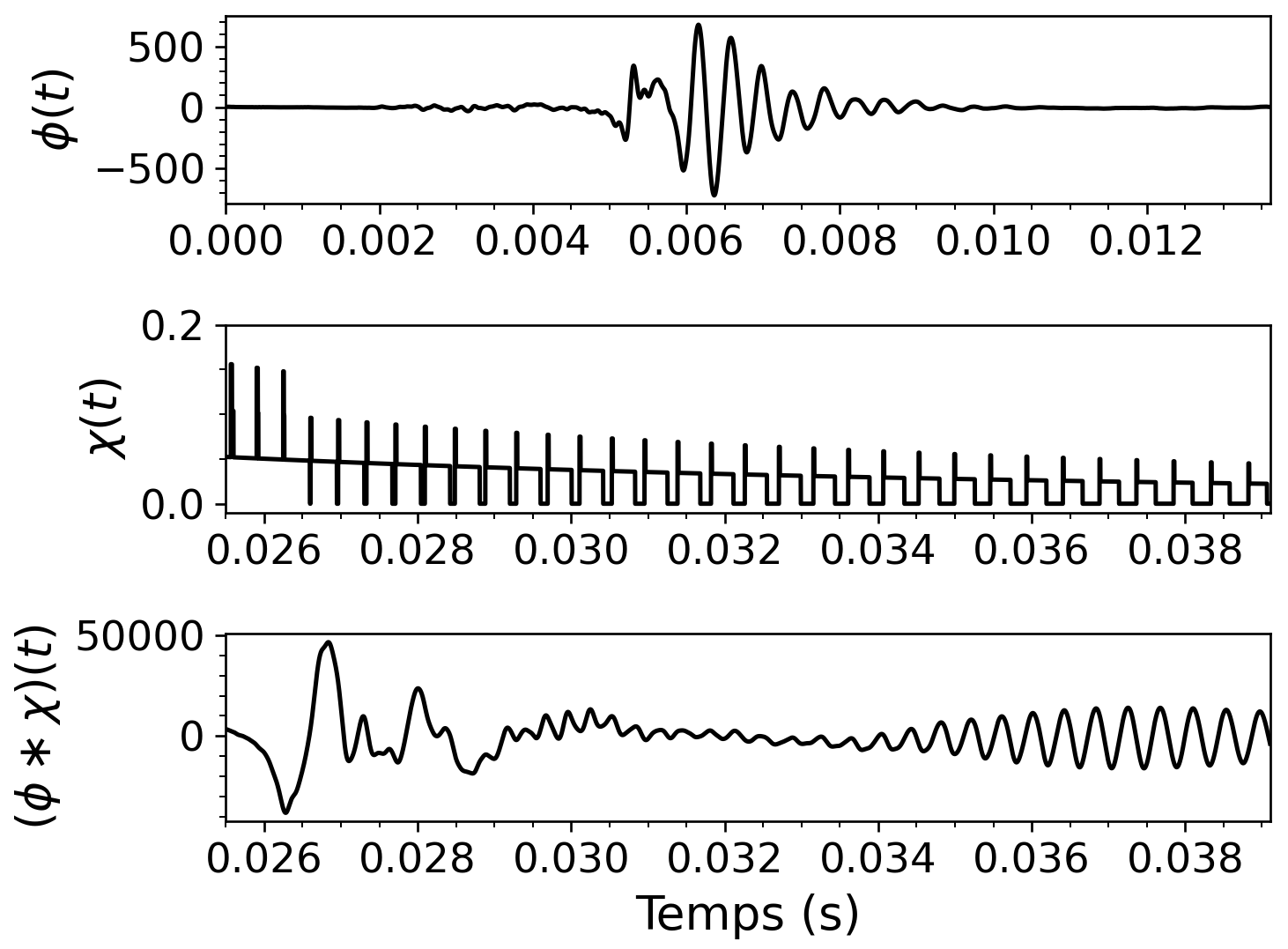
Figure 9 - Haut : courbes de Am(y) et Tm(y) pour m = 1. On voit bien que deux valeurs de y distinctes existent pour 0.0210 ≤ Tm ≤ 0.02105. Bas : fonction de réponse χm(t) pour m = 1. La protubérance au côté gauche démarque les valeurs de t pour lesquelles les ondelettes émises de deux positions y différentes parviennent à l'observateur en même temps.
La fonction de réponse nous informe sur la transformation appliquée par le réseau sur un signal d'entrée - dans notre cas, le profil d'onde φ(t) - pour produire un signal de sortie s(t). Puisque le front d'onde incident possède une étendue temporelle non-nulle, il faut tenir compte du fait que l'observateur reçoit simultanément plusieurs parties de l'onde réfléchies par différents éléments du réseau. Par exemple, si Δt correspond au temps requis à l'onde pour traverser la distance séparant les éléments m et m+1, l'observateur entendra les réflexions χm(t) φ(t) et χm+1(t) φ(t+2Δt) en même temps.
Chaque valeur du signal de sortie est donc l'accumulation d'une infinité d'interactions entre le front d'onde et le réseau, toutes survenues à des positions et instants différents. Cette accumulation prend la forme mathématique d'une convolution entre le signal d'entrée et la fonction de réponse :
s(t) = (φ * χ)(t) = ∫−∞∞ φ(τ) χ(t−τ) dτ
Nous obtenons de ce fait un signal d'amplitude en fonction du temps. Une section de ce dernier est présentée à la Figure 9 aux cotés du reste de la procédure de convolution.
Cependant, puisque s(t) ne signifie pas grand chose sans être joué par un haut-parleur, il faut trouver un moyen de le représenter graphiquement comme un spectre de fréquences qui évolue dans le temps. Ce résultat peut être obtenu en calculant la transformée de Fourier à fenêtre glissante du signal (STFT : Short Time Fourier Transform), définie comme :
S(τ, f) = ∫−∞∞ s(t) w(t−τ) e−i2πft dt
où w(t−τ) est une enveloppe glissante. Contrairement à la transformée de Fourier ordinaire, qui tient compte de l'ensemble du signal simultanément, la STFT opère séquentiellement sur de petits segments du signal, ce qui permet de révéler l'évolution temporelle des fréquences qui composent s(t). Évidemment, en raison du principe d'incertitude temps-fréquence, plus w(t−τ) est étroite, plus la résolution temporelle est fine ; à l'inverse, plus elle est large, plus la résolution fréquentielle s'en trouve améliorée. Dans notre cas, nous ne nous intéressons qu'à la norme de la STFT, c'est-à-dire à |S(t, f)|, qui porte le nom de spectrogramme.
Afin d'assurer un maximum de réalisme, plusieurs clappements de mains ont été enregistrés pour faire office de profils d'onde. Les enregistrements ont été effectués au milieu d'un parc urbain relativement calme, à plus de 50 mètres de toute structure bétonnée susceptible de causer des échos à moins de 300 ms des pulses ; les huit meilleurs ont ensuite été retenus pour le reste de la procédure.
Avant de convoluer les huit φ(t) avec la fonction de réponse, il a été nécessaire d'augmenter artificiellement le taux d'échantillonnage des enregistrements, la résolution temporelle-fréquentielle de la STFT permise par le taux standard de 44.1 kHz s'étant avérée insatisfaisante. Les fichiers audio ont donc été interpolés pour atteindre un taux d'échantillonnage de 2.0 MHz, puis légèrement lissés à l'aide d'un filtre Savitzky-Golay. La fonction de réponse χ(t) a par la suite été générée avec un pas de temps de 0.5 µs (l'inverse du taux d'échantillonnage de 2.0 MHz) puis convoluée avec les enregistrements (Figure 1), donnant huit différents signaux. s(t). Les spectrogrammes de chacun de ces signaux ont été calculés avec une fenêtre w(t) de type Hann d'une longueur de 20 000 points de temps. La moyenne des spectrogrammes (10), |S(t, f)|, constitue le résultat final du modèle convolutif. On constate sur la Figure 10 que les courbes de fn(t) (équation 1) suivent de près les zones chaudes du spectrogramme moyen, mais que seule la diffraction d'ordre 1 contribue significativement au signal.
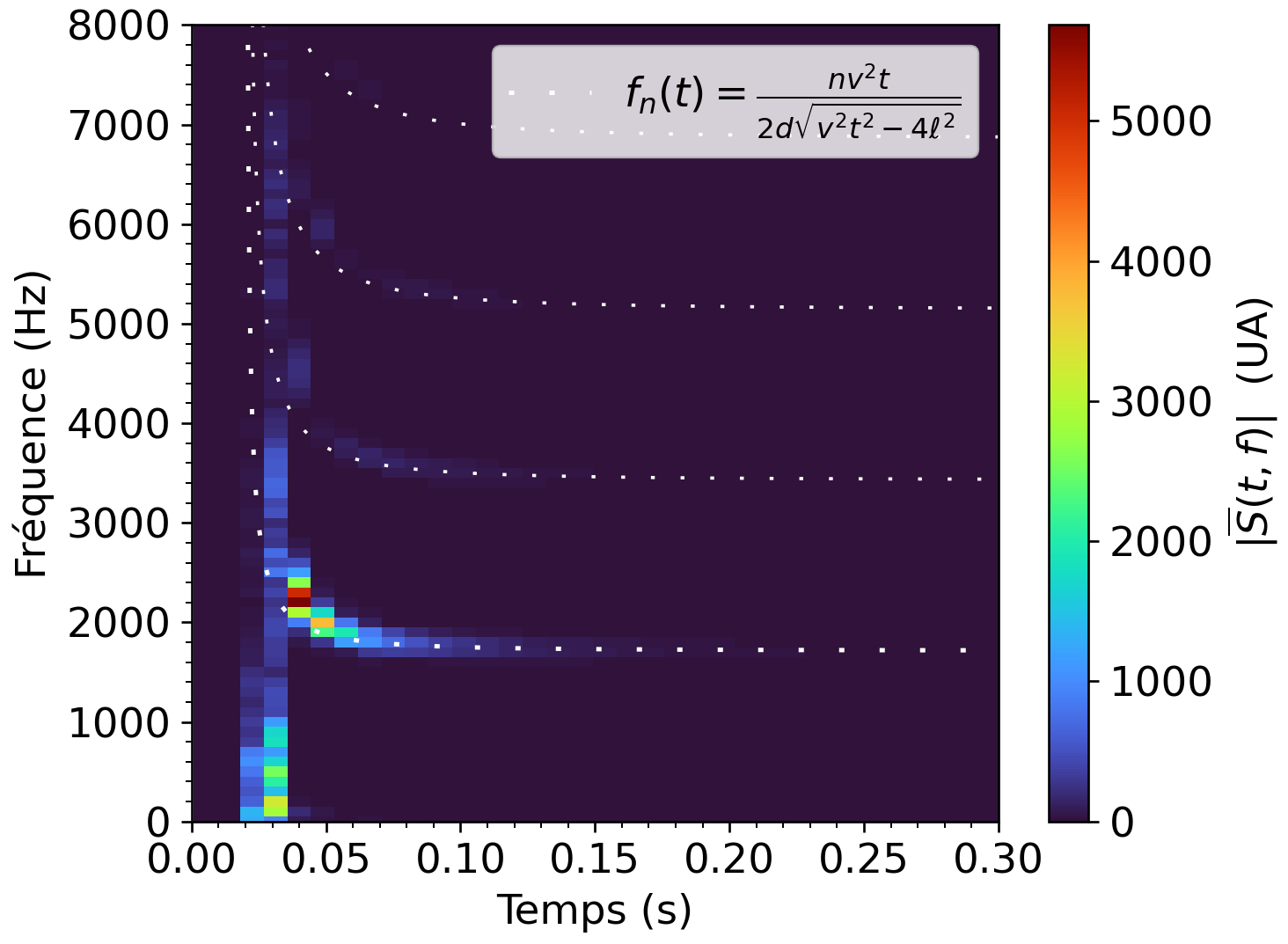
Figure 10 - Moyenne des spectrogrammes des huit pulses. Les traits pointillés suivent la courbe analytique du modèle simple (équation (4)). La zone chaude autour de t=0.03 s et f=0 Hz est en fait l'ordre zéro de la diffraction, c'est-à-dire l'écho du pulse réfléchi vers l'observateur sans subir d'interférence.
Les deux modèles présentés dans cet article fournissent des résultats similaires, le plus important étant le glissement des fréquences vers le bas lors du premier dixième de seconde suivant la génération du pulse. Le premier modèle, basé sur la condition d'interférence constructive, permet de dériver les caractéristiques essentielles du phénomène de diffraction de manière simple et analytique. Le modèle convolutif fournit quant à lui un haut degré de réalisme.
La comparaison des deux modèles permet en fait de sonder la nature même de la diffraction au delà du contexte du phénomène acoustique entendu sur la passerelle du MIL. En effet, la diffraction est la plupart du temps expliquée au moyen de concepts tels que la longueur d'onde et le déphasage. Or, elle émerge naturellement du modèle convolutif, qui demeure tout le long dans le domaine temporel et n'utilise jamais de tels concepts.
Il va sans dire que nous nous penchons ici que sur la modélisation théorique du phénomène ; la seule confirmation de la validité des modèles provient de la comparaison des résultats représentés aux figures 6 et 10 avec l'observation auditive directe. La suite naturelle expérimentale serait donc de tenter de mesurer l'effet directement au moyen d'instruments audio plus sophistiqués que des microphones de téléphones intelligents.
Valeurs numériques
La table 1 contient les valeurs des constantes numériques utilisées dans l'ensemble des calculs.
| Paramètre | Valeur |
|---|---|
| v | 343 m/s |
| d | 0.1 m |
| ℓ | 3.5 m |
| ymin | 0.2 m |
| ymax | 1.2 m |
| hsou | 0.0 m |
| hobs | 1.7 m |
TABLE 1 - Valeurs numériques utilisées dans les calculs.